Probability Basic
in ETC
Probability Density Function & Cumulative Distribution Function
Probability Density Function(PDF)
Random variable X가 연속된 실수 구간에서 값을 취할 수 있는 연속확률변수이고 실수에서의 함수 f가 다음과 같은 성질을 따를 때
\begin{align*}
f_X(x) \ge 0
\end{align*}\begin{align*}
f_X(x) = \int_{-\infty}^\infty f(x)dx = 1
\end{align*}\begin{align*}
P(X \in B) = \int_B f(x)dx
\end{align*}\begin{align*}
P(a\le X \le b) = \int_a^b f(x)dx
\end{align*}f를 X의 probability density function 이라 한다.
이때 PDF는 임의의 한 점에서 확률은 항상 0의 값을 가진다. 이는 4번째 수식에서 a = b 일때 적분값이 0인 것으로 확인할 수 있다. 따라서
P(a\le X \le b) = P(a< X < b) = P(a\le X <b) = P(a< X \le b)의 성질을 갖는다.
Cumulative Distribution Function(CDF)
Random variable X가 연속확률변수이고 PDF f를 가질 때 \begin{align*} F_X(x)= P(X \le x) = P(-\infty \le X \le \infty) = \int_{-\infty}^x f_X(x)dx \end{align*}
인 Fx를 X의 cumulative distribution function 이라 한다.
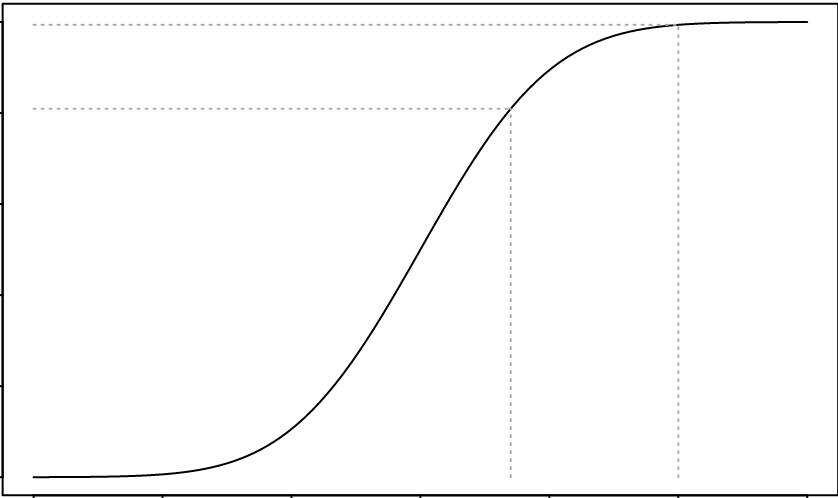
위의 식에서 알 수 있듯 Fx는 fx의 적분으로 시작값은 일반적으로 음의 무한대값을 갖는다.
따라서 CDF가 가지는 성질은 다음과 같다.
F_x(-\infty) = 0F_x(\infty) = 1P(x_1 \le X \le x_2) = F_X(x_2) - F_x(x_1)
Gaussian Distribution, Normal Distribution
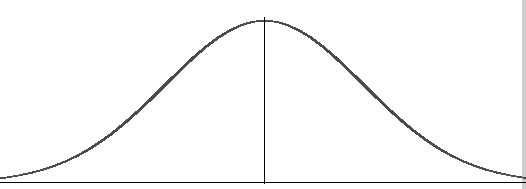
Normal random variable은 PDF에 의해 정의된다. continuous random variable X의 PDF가 다음과 같은 식을 따를 때 \begin{align*} f_X(x) = \frac{1}{\sqrt{2\pi\sigma}}e^-(x-\mu)^2/2\sigma^2 \end{align*}
continuous random variable X를 Gaussian 혹은 Normal 이라 하고 다음과 같이 표기한다. \begin{align*} {X \sim Normal(\mu, \sigma) } \space\space or\space\space{X \sim Gaussian(\mu, \sigma) } \end{align*}
이때 Normal random variable의 성질은 다음과 같다.
- E[X] = μ , var[X] = σ^2
- μ는 임의의 실수값을 가지며 σ는 임의의 0보다 큰 실수값을 가진다.
- Normal r.v의 PDF가 갖는 그래프는 다음과 같은 형태를 보이며 μ에 대해 대칭이다.
- X ~ Normal(μ, σ)일 때 X에 대한 선형함수 Y역시 Normal이다. 이때 Y = aX + b 라면 E[Y] = aμ+b, var[Y]=a^2σ^2 이다.
만약 Z ~ Normal(0,1) 일 때 Z를 Standard Normal 이라 한다.
위의 normal random variable 의 4번째 성질에 의해 임의의 X ~ Normal(μ, σ)를 정규화 하기 위해서
Z = aX + b ~ Normal(0,1)
a = 1/σ , b = -(μ/σ) 로 둔다.
Bayesian Probability
Prior, Likelihood, Posterior
기존의 확률론이 이미 일어났던 일들이 일어난 빈도를 통해 확률을 계산하는 반면 베이지안 확률론은 아직 일어나지 않은 불확실한 일들에 대해 관련있는 확률들을 사용해 새롭게 일어날 사건의 확률을 추론한다.
이때 베이즈 확률에서 앞으로 일어날 사후확률은 사전확률과 가능도의 곱에 비례한다. 이는 P(A|B) = \frac{P(A)P(B|A)}{P(B)} 의 식으로 나타낼 수 있다.
이때 A는 가설, B는 데이터이다.
여기서 사후확률 P(A|B)를 Posterior belief ,
P(A)를 사전확률 Prior belief ,
P(B|A)를 가능도 Likelihood 라 한다.